Different Ways to Attack a QUANT Question — Part 2

Last week we showed the Mathematical (i.e. Algebraic) solution to the Problem below. This week we’ll take a look at a Practical approach. Specifically, we’ll explore the strategy of Plug-Em-Back (a.k.a. back-solving) for the same question.
In order to complete a reading assignment on time, Terry planned to read 90 pages per day. However, she read only 75 pages per day at first, leaving 690 pages to be read during the last 6 days before the assignment was to be completed. How many days in all did Terry have to complete the assignment on time?
(A) 15
(B) 16
(C) 25
(D) 40
(E) 46
Source: Official Guide 2015, PS 119
Solving this question with the Practical strategy of Plug-Em-Back doesn’t mean that you can forego understanding the information presented in the problem, as we discussed in part 1 of this series. You still need to understand the implicit relationship of a rate in this question: (pages / day) x (# of days) = # of pages. And you still need to run through identifying the explicitly stated “players” in the problem, as well as the relationship(s) that exist between them. (See part 1 for more detail.)
Ultimately, your scratch pad might look very similar to how it did for the Mathematical approach up till this point.
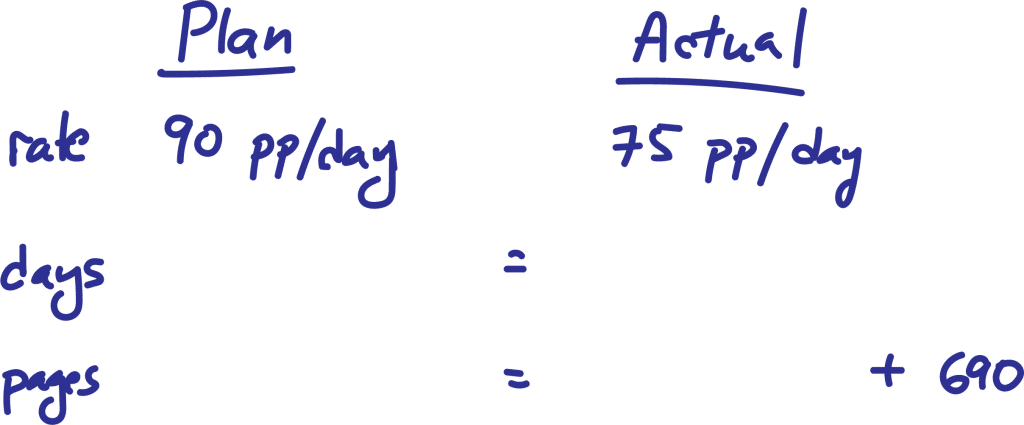
Candidate for Plug-Em-Back
At this point, instead of thinking Algebraically (assigning a variable, coming up with an equation), we will turn to the answer choices. In a problem that is a candidate for the Plug-Em-Back approach, the answer choices will represent a value that can easily be plugged back into the story. The right answer will fit all of the relationships in the story. To make the process easier, it’s important to take the time to capture those relationships in some way. There are some other finer points to the Plug-Em-Back strategy as we’ll see, but that’s the gist of it.
Traditional Approach: C First
One of the downsides of the Plug-Em-Back approach, as you can probably already imagine, is that it can be time consuming. In fact, if you have to do too many computations, it can be a showstopper. To reduce the number of answer you need to check, conventional wisdom says to start with answer C and then to adjust upwards or downwards depending on the outcome (unless of course C is correct.)
This approach can be problematic on the GMAT, however. If C fails, figuring out how an upward or downward change will affect the final outcome might not be easy to predict because the relationships are too involved. Going higher on the answer value (input), can sometimes surprisingly cause the result (output) to become lower. Since the whole idea is to not have to test more than two answer choices, there is another more sure-fire way to “triangulate”.
The BD Approach
It’s the BD approach, and I first heard about it from Kaplan (credit where credit is due). The idea is to test B first. If B doesn’t work, rather than THINK about whether you should go up or down from there, you do D next (you can also switch these, i.e. do D then B). When you check B and D, record something about the result you got from each: e.g. too high, too low. It’s important to note that it’s on the result of the plug that you are commenting, NOT on the answer choice that you are plugging back. By piecing together the results from B and D, you will be able to surmise the correct answer in the manner below.
The Math Itself
Let’s start in this question with 16 days, answer choice B. If 16 days is the correct answer, it will lead to the same value for the total number of pages in the assignment for both the Planned and the Actual scenarios.
The Plan is easier to think about. The total number of pages would simply be the rate of 90 pp/day times the number of days, 16; 90 x 16 = 1440
The Actual is a little tricker, as we saw also in the Mathematical approach. The 16 days are not all spent in the same way. The problem tells us that the last 6 days were spent finishing up the remaining 690 pages, therefore the rate of 75 pp/day was done for only 10 days. The expression for the days read according to the actual scenario then is:
75 pp/day x 10 days + 690 pages = 1440
Jackpot! We got to the same 1440 in both of the scenarios, so answer choice B fits all parts of the story and must be correct.
Note that this idea that the total number of pages must be the same for the Plan and the Actual was key here. This is what I call an implicit relationship (it’s implied by the fact that it’s the same assignment, never stated outright). The relationship was instrumental in solving this question using the Practical approach, just as it was for the Mathematical approach. What we learn from this that regardless of what approach we choose, we still have to capture the relationships. The different approaches dictate what tools we use to do so.
Next week we’ll take a look at this same question using a Conceptual approach.
