
Success on the Quant section of the GMAT involves more than just mastery of the content. Unlike many tests that you may know from your past schooling, the GMAT does not just deliver recycled, slightly-altered versions of past exam questions. Therefore, flexibility and adaptability are paramount.
Almost every GMAT quant question can be solved in more than one way, often even in 3 or 4 different ways. The goal is that for most questions you encounter you’ll be able to consider more than one approach before diving in. Ultimately, the decision of which strategy is right on any given question should be based on your specific skill set and also on the question type along with its specific presentation.
MPC (Mathematical, Practical, Conceptual)
I think of there as being three, mostly distinct – though sometimes overlapping – routes to solving a Quant question: the Mathematical (M), the Practical (P), and the Conceptual (C). Collectively, I use the acronym MPC to refer to them.

The Mathematical most commonly involves the traditional use of Algebraic tools, i.e. writing and/or simplify algebraic equations or expressions, though it is also the term that I would use for applying a Geometry rule or a formula from another area to simply compute something. I would also place, for example, the knowledge and use of exponent rules under this heading.

Next, we have the Practical, the most varied in its make-up. Generally, it entails more hands-on “plug and chug” processes or estimation. There are a number of specific Practical strategies, each of which we will discuss at length in other articles. To name a few, for Problem Solving we have Plug-n-Test, Plug-n-solve, Plug-em-back, and Estimation and for Data Sufficiency, Plug-n-Test.

Finally, the Conceptual involves more abstract reasoning based on mathematical definitions or properties. For example, Number Properties questions can almost always be solved using the Conceptual approach, since these questions test the theory of divisibility, odds & evens, positives & negatives, for which there are rules that can be memorized and applied.
Choose Your Weapon Wisely
To explain these three general strategy paths, I often use an analogy, albeit a somewhat graphic one, of weapons of combat. A well-trained soldier generally must know how to use more than one weapon.
The Knife
The Practical is like a knife, it takes the least amount of training to use, but it can also take the longest to do its job and be the bloodiest (messiest).
The Gun
The Mathematical is the soldier’s firearm. For many, it is the logical first choice and it is an integral part of any soldier’s training. It is effective and can be used without getting your hands “too dirty” (unlike the knife).
The Sniper’s Rifle
Lastly, the Conceptual is the sniper’s rifle. It is the swiftest and most exact, but is the hardest to wield skillfully. It requires the most amount of training to master. Some would even argue that it is not for everyone.
MPC in Action
Now we’ll take a look at a real GMAT question; specifically let’s see how a solution exists to this question in each of the three paths. We’ll start with the Mathematical, covering the Practical and Conceptual in parts 2 and 3 of this article.
In order to complete a reading assignment on time, Terry planned to read 90 pages per day. However, she read only 75 pages per day at first, leaving 690 pages to be read during the last 6 days before the assignment was to be completed. How many days in all did Terry have to complete the assignment on time?
(A) 15
(B) 16
(C) 25
(D) 40
(E) 46
Source: Official Guide 2015, PS 119
One of the main challenges of this question is navigating through the somewhat complex storyline and being able to capture the relationships described in some form. This is something that we’ll have to do regardless of which of the MPC routes we take. When we go the Mathematical route, that form will be Algebra. Algebra of course is made-up of unknowns and equations and/or expressions.
Relationships: Implicit and Explicit
To be successful on this question, you need to recognize, at least on some level, the implicit relationship of a rate in the problem: (pages / day) x (# of days) = # of pages. In the Mathematical approach, this implicit relationship will help us construct the expressions / equation that we need.
Before we turn to the other relationships in this problem – the explicitly stated ones – let’s consider what I like to call “the players”, that is, the different elements that are being discussed and that we will then relate with our equation(s).
Plan vs. Actual
We already covered the elements of the reading rate, i.e. the # of days and # of pages being read. And we already have our implicit formula to relate those (writing that formula on your scratch pad is optional). The other layer to this question is that we have a discussion of Terry’s plan and then we have what actually happened. This is something that I would definitely put down on my scratch pad, with simple column headings – PLAN and ACTUAL.
Ask Good Questions!
After you identify the players the players in your problem (or at least some of them), get in the habit of asking yourself how they relate. So how does Terry’s plan relate to what actually happened? Is something the same between the two (i.e. can something be set equal)?
You might have come up with two answers there: the total number of days to complete the assignment is the same either way as is the total number of pages she needed to read.
If you continue to fill out information in your PLAN and ACTUAL column, it might look like this so far.
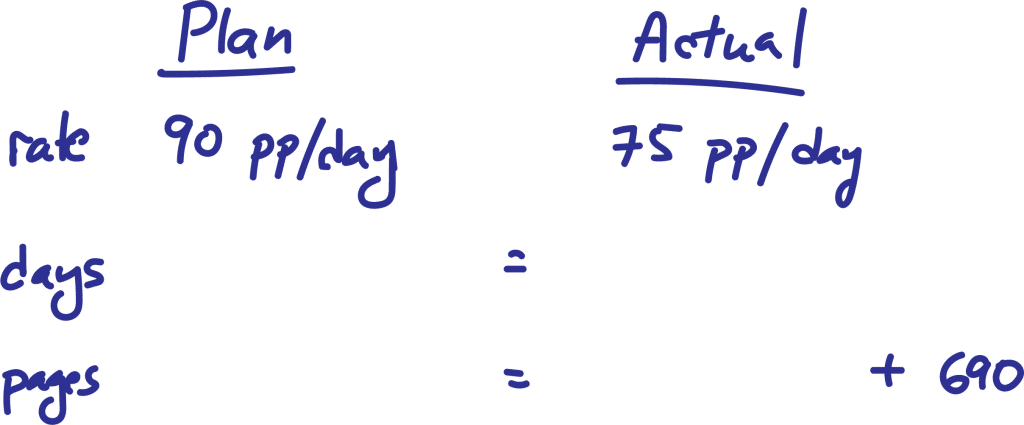
Assigning Your Variable
Using the Mathematical approach, it’s now time to think about assigning a variable. In your high school Algebra class you were probably taught to assign the variable to whatever the question is asking us for, in this case the number of days that Terry has to complete the assignment, let’s say d.
One WARNING for the GMAT though: while this approach can be helpful, it won’t always be. Sometimes it will be much easier to assign a variable to a more intuitive unknown element of the problem. You’ll then use the value you get to work towards whatever they are asking for. In other words, don’t rely exclusively on high school Algebra training there.
Here it does make sense to make the unknown the number of days to complete the assignment, let’s say d, for two reasons. (1) it is common to both the PLAN and the ACTUAL. And (2), d is a logical part of the implicit rate formula. In fact, we’ll learn later that time is often the best unknown in rate questions. And as it turns out, it is also what they are asking for (so high school algebra advice works out)!
Digging for the Equation
Now we want to see if we can more thoroughly fill out our information for the PLAN and ACTUAL. Let’s investigate both from the perspective of the other players in this question: the # of days and the # of pages (we already covered the rates)
The PLAN’s rate of 90 pp/day will be done for all d days.
For the ACTUAL, the d days start off with a rate of 75 pp/day but then before the d days are completed, Terry must speed up in order to complete the assignment. She maintains that faster rate for 6 days to get the last 690 pages done.
Reflecting back on the relationship between PLAN and ACTUAL from earlier, the total number of pages read in both scenarios must be the same. This gives us an opportunity to make an equation!
Two Expressions Equal to Each Other (A Common GMAT Equation)
On the left side of the equation, let’s write an expression for the total number of pages via the PLANNED approach. Then we’ll set it equal to the total number of pages via the ACTUAL on the right side of the equation. Remember, the total number of pages is the same for PLAN and ACTUAL.
As we mentioned, the implicit rate formula tells us to find the total number of pages by multiplying the daily rate by the number of days.
This works great for the PLAN: 90d (i.e. 90 pp/day x d days)
The Hardest Part of the Algebra
The ACTUAL is a little trickier. The rate of 75 pp/day was not done for all d days. The last 6 days were done at a faster rate to compensate (690 in 6 days = 690/6 = 115 pp/day)
What we could do is build the expression for the ACTUAL’s total number of pages in two parts: the all-but-the-last-six-days part and the last-six-days part.
The all-but-the-last-six-days part would be the expression: 75(d – 6). The number of days would be d – 6 because it is 6 fewer than the total number of days, which is d.
The last-six-days part number of pages can just be written as a constant: 690 (no need to right it out as a rate x number of days)
The complete expression for the ACTUAL then is: 75(d – 6) + 690
Since we said the total number of pages is the same for both the PLAN and the ACTUAL, we set those two expressions equal to each other to get the equation: 90d = 75(d – 6) + 690
Your scratch pad now might have looked something like this – less the colors of course!
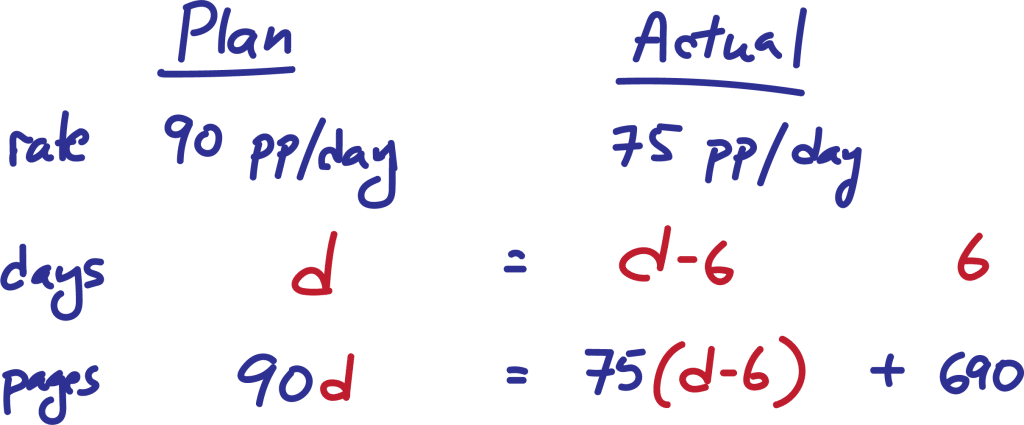
Solve the equation for d and we get d = 16 or answer choice B.
Next week, in part 2 of this series we’ll take a look at how you could have done this question with the Practical method of Plug-Em-Back.
